[ad_1]
Acquisition of flash sequence data
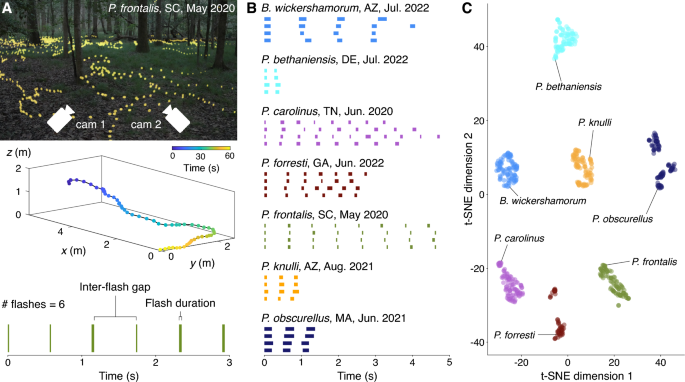
To extract flash sequence data, we perform 3D reconstruction of firefly swarms based on stereoscopic video recordings. Recordings were conducted at specific locations across the country where certain species were known to emerge24. Field researchers placed two spherical (360) GoPro Max cameras at known distances from each other on a level surface (Fig. 1A). Recordings started at dusk when the first flashes were seen, and filmographers performed a simultaneous catch-and-release identification process to acquire ground-truth labels from visual inspection of the individuals present in the swarm. All recordings are made at a frame rate of 30 frames per second. The movies were subsequently processed as described in a previous work22,24 to extract the 3D locations of flash occurrences. From these locations, we apply a simple distance-based linkage method to concatenate flashes into streaks and streaks into trajectories. We consider flashes at consecutive timesteps within a small radius to be part of the same streak; streaks occurring within both 1s and 1m of each other are assumed to come from the same individual and placed in a set of transitively connected streaks called a trajectory. To eliminate noise effects from the trajectory extraction, we threshold the trajectories to eliminate those that only contain one flash. The dataset24 includes ten total species before the application of the thresholding process. Following the thresholding, we also remove any species from the dataset that have fewer than one hundred total trajectories, leaving us with seven species total. Finally, from the trajectories, we extract a binary time sequence by considering the time coordinates of flashes, i.e. a sequence of ones and zeroes where ones represent flashing and zeroes represent interflash gaps. Each element (or bit) of the time series represents a single frame of a video, such that 30 bits represents 1 full second of recording. We further clean the dataset by recognizing that any interflash gaps 1 or 2 bits in length (less than 0.07s) are likely caused by an error in the tracking or trajectorization process, or the firefly briefly being obscured by brush as it moves. These short gaps are replaced by ones to connect the interrupted flash.
This process enables the capture of individual behavior from simple footage of firefly swarms of any species, provided individuals of that species flash frequently enough to meet the threshold standards of the trajectory generation. Our data acquisition procedure highlights the presence of intraspecies behavioral variability, and characterizes this variability by representing flash patterns as distributions (Fig. 4A–C).
The result of this process is 124,503 flash trajectories from the seven species before thresholding, and 65,389 after those with only one flash have been removed. More than half of these are P. carolinus sequences – the majority class. About 1 percent of these are P. forresti and P. bethaniensis sequences – the minority classes. The rest of the classes range between 4 and 14 percent of the total distribution. The dataset comprises binary sequences of between 6 and 1366 bits (0.2s to 45.5s) in duration, each labeled with the corresponding firefly class.
Modeling
We implemented a bespoke neural network architecture with PyTorch to solve our classification problem. For the curious, technical details about the implementation and data-wrangling practices follow. Additionally, all code is open source and available as mentioned in Section “Data availability”.
Neural network architecture
RNNs are a class of neural networks suitable for sequence learning tasks. They are characterized by feedback connectivity and the consequent ability to encode long-range temporal dependencies, such as those intrinsic to firefly flash patterns. The defining computational step of an RNN is the hidden state update, which is a function of the input at the current timestep, \(x^{
(1)
where f is a non-linear activation function, such as hyperbolic tangent, \(W_{hh}\) and \(W_{xh}\) are weight matrices that map hidden-to-hidden (i.e. the feedback connectivity) and input-to-hidden, respectively, and b is a bias term.
Importantly, Eq. (1) enables a recurrent neural network to ingest variable length input sequences, as the update rule can be applied recurrently, which is suitable for firefly flash sequences that are of variable temporal duration. However, if the input duration is sufficiently large–as is the case with some of flash pattern sequences–vanishing gradients will arise when computing weight updates via backpropagation through time (BPTT)29 due to the non-linearity in f, ultimately prohibiting learning.
To address this issue, we leverage an extension to RNNs–gated recurrent units (GRUs)–that introduces gating mechanisms that regulate which information is stored to and retrieved from the hidden state30. These gating mechanisms enable the model to more effectively regulate the temporal context encoded in the hidden state and enables the encoding of longer-range temporal dependencies. Additionally, GRU RNNs are computationally more efficient than other kinds of RNNs like long short-term memory networks (LSTMs), and use fewer parameters, which was a consideration due to our plans for eventual downstream application of the model in real-time population monitoring. Consequently, we implement the model in PyTorch31 as a 2-layer GRU with 128-dimension hidden layers, no dropout, and LeakyReLU activation layers with a negative slope of 0.1.
Data preprocessing
To evaluate our model’s predictive ability on unseen data, we perform 60-fold stratified cross validation to ensure that each sequence in the dataset is used at least once in training and at least once in testing, but never simultaneously. Each fold divides the data into ninety percent training, and ten percent testing, preserving the same class ratios as the original dataset. Due to the severe class imbalance (e.g. some species only comprise 1% of the dataset, whereas others comprise close to 50% of the dataset), we perform random undersampling on the training set of each fold to equalize the class count in the training and validation sets for each fold. This takes the form of a secondary k-fold cross validation procedure to sample from each class until classes are equalized. All the remaining data are used for testing. The reported results are thus the ensemble precision, recall, and accuracy of each model on its respective test set of approximately 30,000 sequences, averaged over the 60 model folds. The ground truth targets are species names; we performed label encoding to transform the targets into machine-readable integers representing each class.
Training and evaluation
We trained the model with the Adam optimizer32 and evaluated performance via cross-entropy loss. During training, we set an early stopping callback that monitored the validation loss with a patience of 50 epochs to prevent overfitting on the training set. Additionally, to alleviate exploding gradients, we applied a gradient clipping of 0.1 to the gradient norms following the procedure recommended in Ref.33. We conducted a hyperparameter sweep over the batch size and learning rate, testing all combinations of batch size \(\in \{8,16,32\}\) and learning rate \(\in \{10^{-3},10^{-4},10^{-5}\}\). We selected the combination that had the highest validation set accuracy on a four-species subset of the data, which resulted in the choice of a batch size of 8 and a learning rate of \(10^{-5}\). No data augmentation was applied during training.
We evaluate the performance of the RNN, along with the signal processing methods described in the following section, on the test data by examining the receiver-operating characteristic (ROC) curves for each species (Fig. 6A–E). Per-species precision and recall are tabulated in Fig. 6F.
Sympatric species experiments
To explore the capabilities of the model when faced with sympatric swarms, we first gave the model a different training regimen. All of the data except for sequences from five days – one day each for B. wickershamorum, P. carolinus, P. frontalis, P. knulli, and P. obscurellus – serve as the training and validation set, and sequences from the five held-out days enter the test set. The five held out days and their codes as referenced in24 are as listed in Table 3. Holding out single days like this ensures that a) the sequences being tested do not occur in the test set and b) the model can identify new sequences on a new day for a species it has already seen before.
We note that P. bethaniensis and P. forresti are excluded from these experiments. This is because for both of these species, holding out one day of data would reduce the total number of sequences in the training set to below one hundred, which is against our recommendation for sufficiency. However, these species remain in the training set, as none of their dates are held out, and thus the model can still predict them during these sympatry experiments.
The goal of these experiments is to vary the different densities of each possible pair of species to test whether the model as trained can capture the presence of each species. This tests whether the model is applicable in future hypothetical scenarios where more than one species may be present in a recording, but each of the species present are already part of the training set in some form. For each experiment, we generated a test set of 400 sequences comprising two species from the holdout days, mixed together at a particular density ratio to create an articifial instance of sympatry. This means that for each iteration of the experiment, the number of sequences for each species ranged from two to 398. We ran 500 iterations of each density ratio for each pair, where each iteration was randomly sampled from the set of sequences corresponding with the held out date. We recorded the true positive rate for each class at each density reported by the model. The results are shown in Fig 3.
Signal processing methods
For the purposes of comparison with the RNN, we implemented four alternative classifiers which use standard signal processing algorithms to compare our dataset against ground truth references for each species. We implement these classifiers using two types of ground truth references: “literature references”, which use flash patterns as previously published in the literature, and “population references”, which are generated by aggregating sequences in our own dataset.
Literature references
“Characteristic” flash patterns for six out of the seven species analyzed in this paper, excluding B. wickershamorum, have been previously recorded and published in the literature. These recorded flash patterns hence served as the primary reference for researchers in identifying signals observed in the field. These reference flash patterns are typically reported pictorially; thus, we convert images to binary-valued time series by computing the relative sizes of flashes and gaps, in pixels. We determine the pixel-to-second conversion to then convert the sequence to a 30 frames per second time series, matching the sampling frequency of our data. We have quantified these variables from published works to underscore the prevalent tendency toward qualitative approximations over quantitative analyses. Flash signals are commonly documented in scholarly articles and monographs through visual representations, frequently drawing from multiple, and occasionally ambiguous, primary and secondary information sources for individual species.
These six reference time series then form the ground-truth comparisons against which our dataset is compared, using the four signal processing techniques described below in Methods Section Signal processing methods. We omit B. wickershamorum as there is currently no published reference pattern.
Population references
We also generate “population references” by aggregating sequences in our own dataset. For each species, we first perform an 80:20 train:test split, similar to the preprocessing procedure performed for the RNN (see above in Methods Section”Data preprocessing”). The population references are obtained by averaging the sequences in each training set. The remaining test data is then classified using the signal processing algorithms described below in Methods Section “Signal processing algorithms”. As with the RNN, we perform \(N = 100\) iterations and take the ensemble average of the performance across all iterations.
Signal processing algorithms
Jaccard index
The Jaccard index compares the similarity between two sets by taking the ratio of the size of the intersection of the sets with the size of the union34 and has found broad application, for example in genomics35. For two binary-valued sequences \((a_m)_{m=1}^{M}\) and \((b_n)_{n=1}^N\) of lengths M and N, respectively, with \(a_m, b_n \in \{0,1\}\) for all m and n, we define the size of the intersection as \(\sum _{i=1}^{\text {min}(M,N)} a_i b_i\), the number of ‘on’ (flashing) bits that occur simultaneously in both sequences. We define the union as \(\sum _{m=1}^M a_m + \sum _{n=1}^N b_n\), the number of on bits for both sequences combined. The Jaccard index can also be evaluated in the same manner for two sequences that are binary-valued. Generally speaking, the intersection can also be thought of as the dot product between the two sequences. To classify a sequence using the Jaccard index, the Jaccard index between a sequence and each species reference is computed, and the softmax of the vector of Jaccard index values is computed to determine a probability of the sequence being from each species. The predicted species is then the argument maximum (arg max) of the softmax vector.
Dot product
The dot product between two sequences is given by the sum of the product of the sequences, i.e. \(\sum _{i=1}^{\text {min}(M,N)} a_i b_i\) for two sequences \((a_m)_{m=1}^{M}\) and \((b_n)_{n=1}^N\) of lengths M and N, respectively. Sequences are then classified by taking the arg max of the softmax of the dot product with each reference.
Dynamic time warping
Dynamic time warping (DTW) is an algorithm that computes the distance between two time series by locally stretching or compressing the sequences to optimize the match. DTW is useful for comparing time series that are qualitatively similar but vary locally in speed and has found significant application in speech recognition36,37,38,39. We implement DTW in MATLAB40 to compute the distance between sequences and species references. Similarly to the other metrics, the predicted species is taken to be the arg max of the softmax of the distances, which is a vector of probabilities that maps to the probability of each label.
SVM
Each flash sequence can be parametrized by 3 values (Fig. 1A): the number of flashes in the sequence, the average duration of each flash, and the average time between flashes (inter-flash gap). We perform support vector machine (SVM) classification in this 3-dimensional space, using a radial basis kernel function.
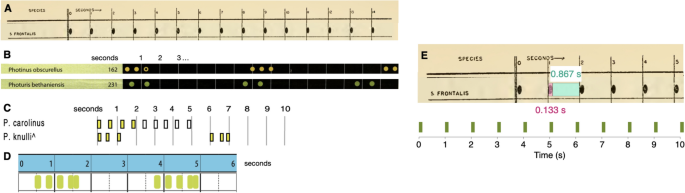
Reference sequences for the firefly species examined in this paper, as previously published in the literature, with the exception of B. wickershamorum. (A) Reference pattern for P. frontalis from Barber, 195141. (B) Reference patterns for P. obscurellus and P. bethaniensis from Faust, 20177. (C) Reference patterns for P. carolinus and P. knulli from Stanger-Hall and Lloyd, 20158. ( D) Reference pattern for P. forresti from Fallon et al., 20226. (E) Illustration of extracting P. frontalis sequence from literature pattern (top) and converting to time series (bottom).
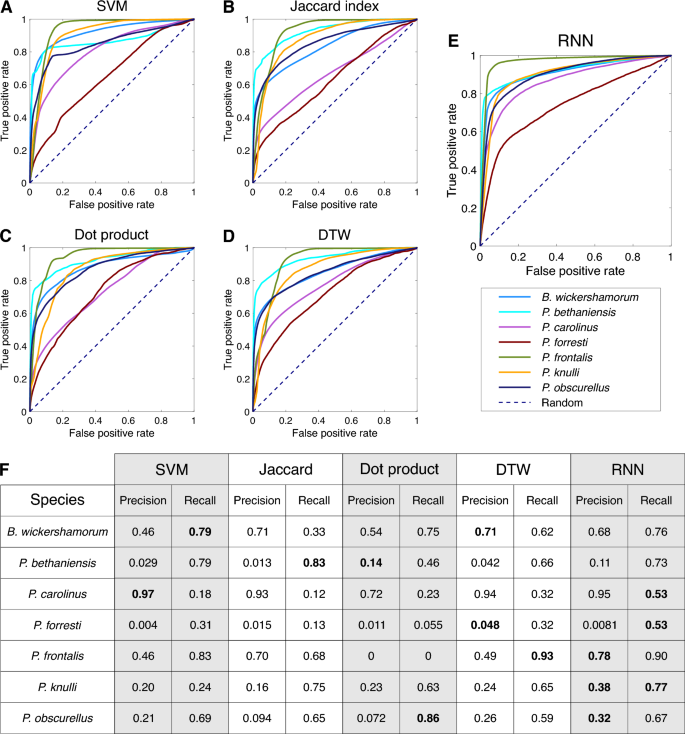
Per-species ensemble of classification results. (A–E) Receiver operating characteristic (ROC) curves representing the true positive rate (TPR) as a function of the false positive rate (FPR) across all model thresholds of classification, labeled by method. All non-RNN classification methods are conducted using population references. (F) Table of per-species precision and recall across all surveyed methods (N=100). Bold statistics in the table represent the highest performer for each metric and species. Precision values for P. bethaniensis and P. forresti are low because these two species represent the classes with the fewest number of samples, and so there is a very small amount of true positive values. However, these still greatly exceed what would be expected by chance (0.001 and 0.006, respectively). The high recall for these classes indicates that the true positives are correctly captured.
Characterization
The data acquisition procedure is not without noise, so we perform filtering to produce accurate quantitative characterization of flash phrases that falls in alignment with previous literature observations. We leveraged the ability of the RNN to distinguish between sequences by choosing the sequences which the RNN scored highest as the top one hundred most confident classifications for each species. This subset acts as the dataset on which characterization exercises are performed for Fig. 1B and Fig. 4. The procedure is as follows:
-
1.
Initialize the empty list c
-
2.
for each i sequence in the test set D:
-
(a)
Run a forward model step
-
(b)
Let p = the maximum probability in the resulting vector of softmax predictions
-
(c)
If the index of p corresponds with the correct label, add the pair (p, index) to the list c
-
(a)
-
3.
Sort c by probability p and choose the top 100
-
4.
Index into the dataset D using the associated indices of the top 100 probabilities to produce the subset
Characterizing in this way leverages the variability in the entire dataset by training the predictive classifier, then asks the predictive classifier only for what it is most confident about in order to filter out sequences that may be missing flashes or exhibiting patterns that are far from the statistical norms of the species.
[ad_2]
Source link