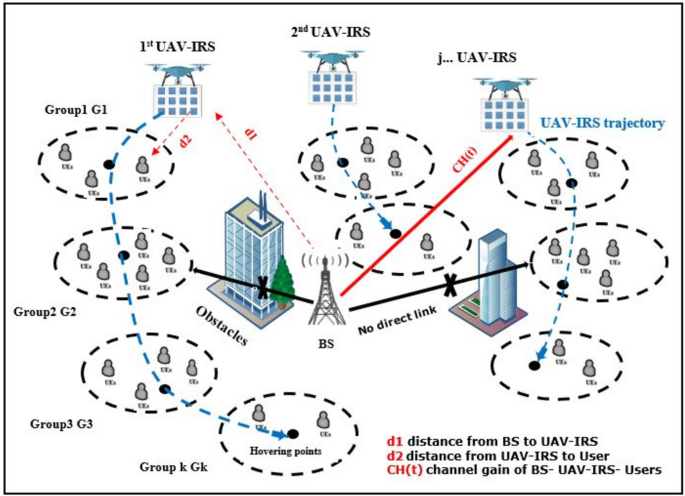
Initially, in this section, the network model, the channel model, the UAV-IRS model, the energy consumption model of UAV-IRS, the obstacle model and the area size decomposition are introduced.
Network model
In this section, a downlink transmission UAVs-IRS aided THz wireless communication system is studied. We consider the downlink system model of a wireless network operating in the THz (0.3–10 THz) bands, to support outdoor applications, which consists of one BS operating in THz band that located at midpoint the urban area denoted by \(A\). Also, number of Ground Users (GUs) are denoted by \(N\) which are uniformly distributed in the coverage area. While number for UAVs-IRS is denoted as \(M\). The position of UAV-IRS \(j\) is dispatched from the midpoint area, and UAVs-IRS will hover for some time above each group of users at Hovering Points (HO), to cater the users within that group. We assume that \(\text{G }=\left\{{\text{G}}_{1,}\dots . {,\text{G}}_{K}\right\}\) where \(K\) is number of groups of users. It is assumed that direct links between BS and the GUs are obstructed by building or other obstacles environmental. The positions of the obstacles are assumed to be known, which is out of the scope of consideration in this paper. Communications between BS and GUs have been assisted by UAV-IRSs which are considered to be using Uniform Planar Array (UPA). The number of IRS reflective elements are \(I={I}_{x} {I}_{y}\) where \({I}_{x}\) and \({I}_{y}\) are IRS reflecting elements numbers along the x-axis and y-axis respectively. Assume that rotary-wing UAV-IRS supports the flying hovering mode without taking acceleration and deceleration into account. Specifically, the UAV flies to the hovering points with a constant speed and hovers at these points with static status for servicing all users in groups.
Three-dimensional Cartesian coordinate system used to model UAV-IRS \(j\) in THz network, considered the coordinate for BS can defined as \({q}_{B}=\left({x}^{\text{BS}}= 0,{y}^{\text{BS}}= 0,{h}^{\text{BS}}\right)\), where \({h}^{\text{BS}}\) is BS altitude and coordinates of user \(N\) is \({q}_{n}=({x}_{n}^{\text{GU}},{y}_{n}^{\text{GU}},{h}_{n}^{\text{GU}})\), UAVs-IRS \(j\) coordinates is \({q}_{j }=\left({x}_{j}^{\text{UAVIRS}}\left(t\right),{y}_{j}^{\text{UAVIRS}}\left(t\right),{h}_{j}^{\text{UAVIRS}}\right)\), respectively.
The system architecture of UAV-IRS assisted THz wireless communication network is shown in Fig. 1. UAVs-IRS takes off from an initial point at the middle area \({\text{G}}_{1}\), determines the location for hovering point at Group 1 \({\text{G}}_{2}\) that will be visited first. UAV-IRS repeats this procedure until servicing all users for all groups is completed, and flies back to \({\text{G}}_{1}\).
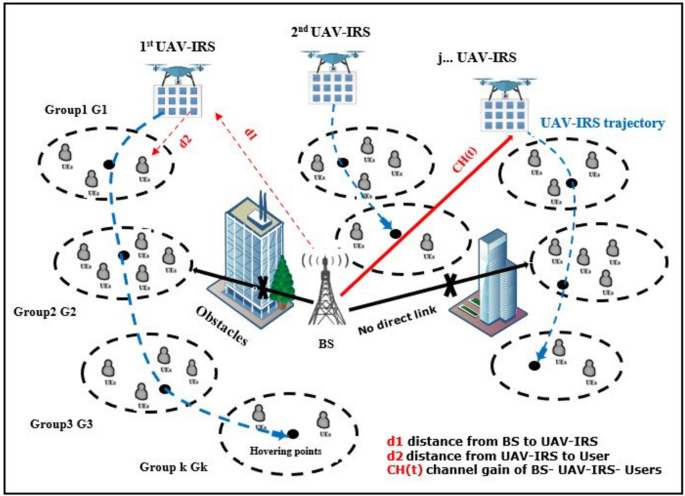
The illustration of system model.
Channel model
As the key to understanding the THz band and laying out fundamentals for communications network, THz multipath channel model characteristics are essential for system design and performance evaluation. Channel models may include parameters such as sparse multipath loss, molecular absorption loss, diffuse scattering and specular reflection30,31. Consequently, channel transfer function is expressed as follows:
$$H\left( {f,d} \right) = \frac{c}{4\pi fd}e^{ – 0.5k\left( f \right)d}$$
(1)
where the term \({e}^{-0.5 k\left(f\right)d}\) indicates the channel path-loss due to the molecular absorption and the concentration of water vapor molecules in the air32, and \(c\) is speed of light, \(f\) is the carrier frequency. The \(k\left(f\right)\) represents the absorption loss coefficient that is based on the transmission frequency and expressed as:
$$k\left(f\right)=\frac{P}{{P}_{\text{stp}}}\frac{{T}_{\text{stp}}}{T}{\sum }_{n,g}{Q}^{n,g}{\sigma }^{n,g}\left(f\right)$$
(2)
where \(n,g\) is denoted the gases and all their isotopologue existing in air, respectively. The standard temperature is \({T}_{\text{stp}}\), \({P}_{\text{stp}}\) denotes the standard pressure, \(T\) represents the temperature, and \(P\) is the pressure. The transmission environment is indicating as \({Q}^{i,g}\), and \({\sigma }^{n,g}(f)\) represents the number of molecules per unit volume at frequency \(f\)28. Euclidean distance from BS to the UAV-IRS and from UAV-IRS to GUs represents as \(d =\) \({d}_{1}+{d}_{2}\), where \({d}_{1}\) is distance between BS and first reflector of IRS, and \({d}_{2}\) is the distance between first reflector of IRS and GUs, can be expressed as follows:
$${d}_{1}=\sqrt{\left({x}^{\text{BS}}-{x}_{j}^{\text{UAVIRS}}\left(t\right)\right)+\left({y}^{\text{BS}}-{y}_{j}^{\text{UAVIRS}}\left(t\right)\right)+\left({h}^{\text{BS}}-{h}^{\text{UAVIRS} }\right)}$$
(3)
$${d}_{2}=\sqrt{\left({x}_{j}^{\text{UAVIRS}}\left(t\right)-{x}^{\text{GU} }\right)+\left({y}_{j}^{\text{UAVIRS}}\left(t\right)-{y}^{\text{GU} }\right)+\left({h}^{\text{UAVIRS}}-{h}^{\text{GU}}\right)}$$
(4)
Coherence time
Coherence time is a temporal measure of the channel’s coherence. It is referring to measure of the time duration over which the wireless channel impulse response remains constant sufficiently for effective communication33. In the THz frequency band, due to the extremely high frequency and dynamic environments, the coherence time is typically very short. Particularly, we would like to clarify our system model can be acquired with the longer coherence time, which increases the accuracy of the distance determination. To manage coherence time effectively in system model to ensure reliable communication, we utilize a fixed user in multiple UAV-IRS scenarios in THz network offers several advantages including stability, typically experiencing more stable channel conditions since they are not moving relative to the network infrastructure.
Transmission strategy
In the transmission strategy, UAV-IRS is used as the air relay to transmit information between BS and GUs, assuming that direct links are blocked due to blockage in the environment. The wireless signal is transmitted to the receiver through channel transfer function in THz band.
Additionally, the adaptability of UAVs-IRS allows them to relocate by sensing channel characteristics to improve actively channel conditions. Consequently, channel conditions are actively modified compared with fixed infrastructure communication. IRS is equipped with \({I}_{x} {I}_{y}\) elements of phase shift to establish the reflection communication link among BS and GUs through regulating IRS phase shift. Thus, the channel gain of BS—UAV-IRS—GUs can be represented by34:
$$G \left(\text{t}\right)=g \left(\text{t}\right) {e}_{t }\left(\text{t}\right) \Phi { e}_{r }(\text{t}{)}^{T}$$
(5)
where, \(\Phi\) is beamforming matrix of IRS which is the diagonal phase shift matrix, defined as: \(\Phi =diag[{w}_{1}{e}^{j{\phi }_{1}}, {{w}_{2} e}^{j{\phi }_{2}},\dots .. {{w}_{n} e}^{j{\phi }_{n}} ]\) where \({w}_{n}\in \left[0, 1\right]\) is an amplitude reflection coefficient of the reflective element of IRS, \(\phi \in \left[0, 2\pi \right]\) is the phase shift of IRS element, and \(j\) is a complex number’s imaginary unit.
\({e}_{t }\left(\text{t}\right)\) indicates the transmit vector from BS to UAV-IRS and \({e}_{r }(\text{t})\) is received vector from the UAV-IRS to GUs, respectively. Finally, the cascade channel of BS- UAV-IRS- GUs link as follows35:
$$g\left(t\right)=\frac{c}{8\sqrt{{\pi }^{3 } }f {r}_{t }\left(t\right) {r}_{o }\left(t\right)}{e}^{-j2\pi f \frac{\left( {r}_{t }\left(t\right)+{r}_{o }\left(t\right)\right)}{c}} {e}^{-\left(-0.5k\left(f\right)\left({r}_{t }\left(t\right)+{r}_{o }\left(t\right)\right)\right)}$$
(6)
where, \({r}_{t }\left(t\right)\) is the transmission vector array from BS to the first component of UAV-IRS, and \({r}_{o }\left(t\right)\) is the transmission vector array from first component of UAV-IRS to GUs.
UAV-IRS model
Without loss of generality, we assumed UAVs-IRS \(j\) fly with fixed altitude \(h\), moving at a constant speed \(v\) in (m/s) and not exceeding maximum speed \({v}_{\text{max}}\). At each time slot period \({\updelta }_{t}\), it can move with the maximum distance as \({d}_{\text{max}}={v}_{\text{max}}{ \delta }_{t}\). In each time slot \(t\), UAV-IRS will move with flying action determined by an angle of \({\upmu }_{t}\in [\text{0,2}\pi\)], and a distance of \({\text{d}}_{t}\) ∈ [0, \({\text{d}}_{max}\)]. This work only addresses 2D trajectory optimization, as the environment is dominated by high-rise buildings that would be necessary long climbing phases to be overflown. Based on the movement of UAV-IRS, the position of UAV-IRS will change after each time slot \(t\), and the moving distance will be calculated as follows:
$$x_{j}^{{{\text{UAVIRS}}}} \left( t \right) = x_{j}^{{{\text{UAVIRS}}}} \left( {t – 1} \right) + v\left( t \right) \delta_{t} \cos \varphi_{t}$$
(7)
$$y_{j}^{{{\text{UAVIRS}}}} \left( t \right) = y_{j}^{{{\text{UAVIRS}}}} \left( {t – 1} \right) + v\left( t \right) \delta_{t} \sin \varphi_{t}$$
(8)
where \(\varphi_{t}\) is UAV-IRS direction at time slot \(t\) from UAV-IRS \(j\) to the users \(n\). Also, we assumed that the trajectory of UAV-IRS \(j\) can visit all sequence of locations of stop points \({\text{G}}_{j}\) in \({Q}_{j}({T}_{j}^{F})\) selected as:
$${Q}_{j} ( {T}_{j}^{F} ) = [ {x}_{j}^{\text{UAVIRS}}
(9)
This paper assumes that the entire process of deployment UAVs-IRS is divide into T time slots of unequal length, and each time slot \(t\) with sufficient slot length \({\updelta }_{t}\). For ease of exposition, we divide it into three components. So, the completion time of UAV-IRS trajectory is directly related to the summation of the flying time, the flying hovering, and operation time of UAV-IRS \(j\). The overall completion time of UAV-IRS \(j\) is as follows:
The first phase UAVs-IRS processing time \({T}_{j}^{pro}\)
Based on the group’s current location and avoiding obstacles, UAVs-IRS calculates the next optimal location, which includes the planning duration time, which varies depending on the complexity of the mission, and the trajectory execution (trajectories are designed based on the specific requirements of a mission, taking into account factors such as optimal UAV-IRS location, hovering points changes).
The second phase UAVs-IRS flying time \({T}_{j}^{F}\)
Time required for UAV-IRS to fly from the present hovering point to the next new hovering point. In other words, we need to decide the visit order of the hovering point to minimize the flight distance of UAVs-IRS and thus minimize the flight time. Let \({\text{G}}_{1}\) and \({\text{G}}_{K}\) be the optimal starting and ending group positions of UAV-IRS respectively. Moreover, the order of visiting the hovering points is expressed as \({\text{G}}_{1},\dots .{\text{G}}_{k}\) and let the order set \(\text{G}\) to present UAV-IRS whole trajectory be:
$$G = \left\{{\text{G}}_{1},\dots \dots .. {,\text{G}}_{k} \right\}$$
(10)
According to UAV-IRS speed \(v\), it is possible to determine UAV-IRS flying Time \({T}_{j}^{F}\) which can be represented as:
$${T}_{j}^{F}=\sum_{i=1}^{\text{k}} \frac{d\left({\text{G}}_{i}-{\text{G}}_{j}\right)}{v}$$
(11)
where \(d\left({\text{G}}_{i}-{\text{G}}_{j}\right)\) is the distance function that calculates the distance between hovering points \({\text{G}}_{i}\) and \({\text{G}}_{j}\).
The third phase UAVs-IRS hovering time \({T}_{j}^{hov}\)
After UAVs-IRS selection of the hovering point of each group, and UAV-IRS visiting order to these hovering points. In this case, the hovering time of UAVs-IRS is the time it takes to associate with the users through communicating and collecting the data and serving users inside the groups.
Let \({T}_{j}^{hov}\) be the hovering time that the users in the k-th cluster communicate with UAV-IRS, which can be expressed by:
$${T}_{j}^{hov}=\frac{D}{{R}_{j}
(12)
where D is total data transmitted for users, and \(R
(13)
where \(\uppsi\) the network experiences interference, the channel gain is \(\text{CH}\left(\text{t}\right)\), \({\text{P}}_{\text{j}}\) is transmit power from UAV-IRS to their GUs, \({B}_{j}\) is the total THz-bandwidth, and \({\upsigma }^{2}\) is the additive white Gaussian noise (AWGN).
Then, \(k\left(f\right)\) the absorption loss coefficient, and the distance from BS—UAV-IRS—GUs represents \(\text{d}\). The following total mission completion time for UAVs-IRS \(j\) as follows:
$${T}_{j} ={{T}_{j}^{F}+T}_{j}^{hov}+{T}_{j}^{pro}$$
(14)
The UAV-IRS responds to environment and makes decisions swiftly, so the processing and decision time is negligible compared to the flight time and hovering time of UAV-IRS, the division of time slots is displayed in Fig. 2 below.
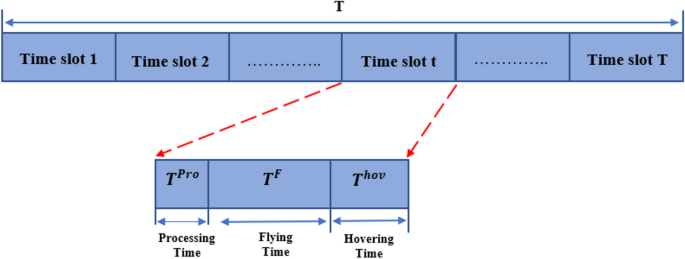
Diagram of time slot division.
Energy consumption model
There are many factors that are involved of UAV-IRS energy consumption such as the energy during operations such as flying energy to keep UAV-IRS mobile and hovering energy. Regarding for the power consumption of the UAVs-IRS, it mostly consists of the communication-related power consumption and propulsion power consumption. The former primarily consists mostly of signal, circuitry, reception, and processing consumption, which is negligible compared with the propulsion power consumption. Therefore, the propulsion power consumption measures the energy consumed to fly or hover over UAVs-IRS. In general, energy consumption depends not only on UAVs-IRS velocity but also on its acceleration and deceleration. It should be noted that ignored the energy consumption during the acceleration and deceleration of UAVs-IRS37, which makes sense in reasonably where the acceleration and deceleration speed or acceleration/deceleration duration is minimal38. Therefore, power consumption of rotary-wing UAV-IRS flying with speed \(v\) represents as:
$$P ={P}_{0}\left(1+\frac{3{v}^{3 }}{{U}^{3 }}\right)+{{P}_{1} }\sqrt{{1+\frac{{v}^{4 }}{4 {v}_{0}^{4}}-\frac{{v}^{2}}{4 {v}_{0}^{2}}} }+\frac{{d}_{0 }\rho s{v}^{3 }A}{2}$$
(15)
where \({P}_{0}\) and \({{P}_{1} }\) are blade profile power and induced hovering power state, respectively which are two constants linked to the physical parameters of the UAV-IRS. The tip speed of the rotor blade represents \(U\), average rotor-induced velocity when hovering denotes \({v}_{0}\), the fuselage drag ratio is \({d}_{0}\), the rotor stiffness denotes as s, air density is ρ, and \(A\) represents the rotor disk area. The relevant parameters are explained in details in Table 1. By substituting \(v=0\) into (15), the hovering power consumption which is a finite value depending on the air density, aircraft weight, and rotor disc area, can be expressed as:
$${P}_{h}={P}_{0}+{P}_{1}$$
(16)
As can be seen from (15) the propulsion power consumption of rotary-wing UAVs-IRS consists of three parts: induced, blade profile, and parasite power. The blade profile power and parasite power, increase cubically and quadratically, needed to control profile drag of blades and fuselage drag, respectively. However, induced power is needed to overcome the induced drag of the blades, that decreases with \(v\).
After that, the total energy consumption of UAV-IRS used to determine the general consumption of energy denoted by \(E\) during flight which is the sum of hovering energy \({E}_{j}^{hov}\) and flying energy \({E}_{j}^{F}\), and we deploy more than one UAV-IRS, so the fixed cost (e.g., take off or land in, maintenance) may incur \({E}_{j}^{pro}\).
Based on the above analyses, total energy consumption of proposed algorithm is expressed as:
$$E=\sum_{j=1}^{M}{{E}_{j}^{F}+E}_{j}^{hov}+ {E}_{j}^{pro}$$
(17)
wherein energy consumption of UAV-IRS flying \({E}_{j}^{F}\) given as follows: \({E}_{j}^{F}= {T}_{j}^{F}* {P}^{F}\) , where \({P}^{F}\) is the flight power of UAV-IRS during flight14, and \({T}_{j}^{F}\) is the amount of time the drone spent flying overall.
Moreover, \({E}_{j}^{hov}\) the energy consumption of hovering time is given as follows: \({E}_{j}^{hov}= {T}_{j}^{hov}* {P}^{hov}\), where \({P}^{hov}\) is the UAVs-IRS hovering power, and \({T}_{j}^{hov}\) hovering time, respectively.
Obstacle model
In this paper, we assumed that the sizes and locations of the obstacles are known, since each blockage is represented as a rectangle with dimensions being the length, the width, and height of the obstacle, respectively. Obstacles can be measured by 3D point. In particular, we consider several obstacles, and their model are referred to in39. After that, GUs will be deployed randomly on the area size with these obstacles.
Area decomposition
In this subsection, large area is decomposed depending on the available number of UAV-IRS. Aim to prevent UAVs-IRS from under-collision and avoid obstacles in environment, and balance the energy consumption for different UAVs-IRS. In order to achieve better coverage and improve the system’s performance, the area is divided into various groups. As mentioned previously the number of UAVs-IRS is not predefined in the system. Inspired by the work in37, a modified k-means algorithm was used for divide users into various groups that are classified based on shortest distance criteria that allocate users to groups and can apply data rate constraints in accordance with predetermined requirements.