QRM-MLD
QR decomposition with the M-algorithm for maximum likelihood detection plays a vital role in reducing latency in 5G networks. In 5G, low latency is critical for real-time applications, such as autonomous vehicles and remote surgery. QR decomposition efficiently mitigates the latency by enhancing the accuracy of symbol detection. Decomposing the channel matrix allows for a more precise estimation of the transmitted symbols even in the presence of interference and noise. This reduces the need for retransmission and reprocessing of data, thereby lowering the communication latency. Consequently, 5G networks benefit from improved reliability and faster data transmission, ensuring that critical applications operate with minimal delay and meeting the stringent latency requirements of emerging technologies44. Consider the Massive-MIMO (M-MIMO) system shown in Fig. 7. The received signal in MIMO systems refers to the combined signals received at multiple antennas that exploit spatial diversity for improved communication performance. The received signal in M-MIMO can be represented as
$$Z=Hy+{\omega }_{n},$$
(1)
where Z is the received signal given by \(Z={\lceil{Z}_{1} {Z}_{2}, . . . , {Z}_{m}\rceil}^{T}\), y represents the transmitting signal from \({n}_{th}\) antenna: \(y={\lceil{y}_{1} {y}_{2}, . . . , {y}_{n}\rceil}^{T}\), \({\omega }_{n}\) is the noise, and h is the response of the channel given by Ref.45.
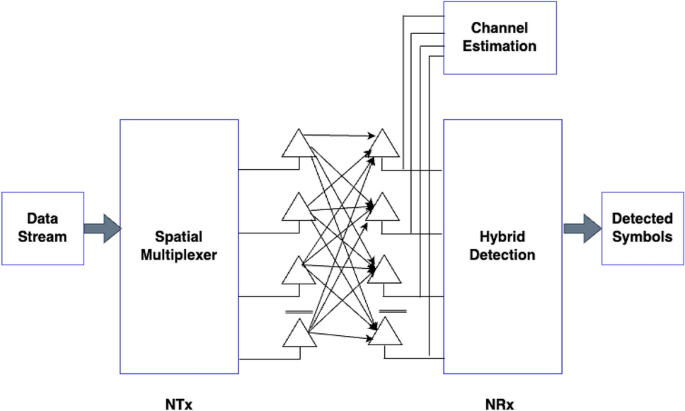
MIMO with hybrid detection.
$$H=\left[\begin{array}{ccc}{h}_{\mathrm{1,1}}& \cdots & {h}_{1,m}\\ \vdots & \ddots & \vdots \\ {h}_{n,1}& \cdots & {h}_{n,m}\end{array}\right].$$
(2)
The channel response matrix H in MIMO systems is crucial for characterizing wireless channels, enabling efficient beamforming, spatial multiplexing, and diversity techniques for enhanced communication performance and throughput. QRM-MLD involves optimizing the signal detection to maximize the likelihood of the received symbols given the observed data. The conventional QRM-MLD algorithm can be expressed as46
where H denotes the channel response, which is split into \(n\times n\) unitary matrix (Q) and \(m\times m\) triangular matrix (T) given by47:
$$T=\left[\begin{array}{ccc}{t}_{\mathrm{1,1}}& \cdots & {t}_{1,m}\\ \vdots & \ddots & \vdots \\ 0& \cdots & {t}_{m,m}\end{array}\right].$$
(4)
The Eq. (4) in QRM-MLD assists in reducing computational complexity by facilitating efficient relay selection and symbol detection, optimizing performance, while minimizing processing requirements in MIMO systems. In the M-MIMO framework, state \(n\le m\) must satisfy to obtain a unique solution. In this equation, we consider \(n=m\) and convolve Eq. (1) with QH as follows:
$$\overline{Z }={Q}^{H}\left({H}_{y}+{\omega }_{n}\right)={T}_{y}+\overline{{\omega }_{n}}.$$
(5)
The received signal (\(\overline{Z })\) comprises the combined transmissions from multiple antennas, whereas noise (\(\overline{{\omega }_{n}}\)) refers to unwanted interference or disturbances affecting the received signal quality. It is noted that the \(\overline{Z }\) and \(\overline{{\omega }_{n}}\) are defined as48
$$\overline{Z }=Z{Q}^{H},$$
(6)
$$\overline{{\omega }_{n}}=Z\overline{{\omega }_{n}},$$
(7)
Further, the M algorithm is applied to Eq. (5) to obtain the sequence of transmitting elements: \({\lceil{y}_{1} {y}_{2}, . . . , {y}_{n}\rceil}^{T}.\) Once the sequence of the transmitting element is selected, ML is used to determine the transmitted signal elements. Initially, the selection of the transmitting signal element \({y}_{n}\) was completely demonstrated. ML is determined to obtain a constellation of all the signal elements. Hence, S-time computations are executed as follows49:
$${\left|\overline{{x }_{n}}-{T}_{n,n}{y}_{n}\right|}^{2}.$$
(8)
From Eq. (8), the N nodes that correlate with the minimal N value are adopted, and the rest of the nodes are rejected. The designated node is dilated into \(\left|S\right|\) nodes and \(N\times \left|S\right|\) computations are executed as follows50:
$$\bigg\Vert {\left[\begin{array}{c}\overline{{x }_{n-1}}\\ \overline{{x }_{n}}\end{array}\right]-\left[\begin{array}{cc}{t}_{n-1,n-1}& {t}_{n-1,n}\\ 0& {t}_{n,n}\end{array}\right]\left[\begin{array}{c}{y}_{n-1}\\ {y}_{n,s}\end{array}\right]\bigg\Vert }^{2}.$$
(9)
The Eq. (9) can be also written as50:
$${\left|\overline{{x }_{n-1}}-{t}_{n-1,}n-1{y}_{n-1}-{t}_{n-1},n{y}_{n,}S\right|}^{2}+{\left|\overline{{x }_{n}}-{t}_{n,}n{y}_{n,s}\right|}^{2}.$$
(10)
Here \({y}_{n,s}\) first selects the contender in the initial step. In addition, the N entrant element is chosen for transmitting signal \(\left[{y}_{n-1}{ y}_{n}\right]\), which represents the trivial N parameter from the \(N\times \left|S\right|\) values. Likewise, the N entrants signal elements for \(\left[{y}_{n-2,}{ y}_{n-1},\dots {y}_{n}\right], . .. \left[{y}_{1},{y}_{2},. . . {y}_{n}\right]\) are considered at every period. Finally, the signal elements \(\left[{y}_{1,}{ y}_{2},\dots {y}_{n}\right]\) are determined as the optimal approximated evaluated transmitted signals. The intricacy of the traditional QRM-MLD is less as compared with the ML. However, the prototype implementation requires more computation, leading to high complexity. The QRM-MLD suffers from several drawbacks. Firstly, it’s computationally intensive, demanding substantial processing power and time. Secondly, it’s sensitive to initialization, potentially leading to convergence to local optima. Additionally, it’s prone to numerical instability when dealing with ill-conditioned matrices. To improve detection, one can employ advanced optimization techniques like stochastic approximation or evolutionary algorithms, enhancing convergence and robustness. Furthermore, incorporating regularization techniques can mitigate numerical instability issues. Employing parallel computing can also expedite computation, making it more feasible for real-time applications.
ZFE
It is considered a simple detection method that is utilized in the M-MIMO framework. The primary aim of the ZFE is to obtain optimal signal detection in the presence of interference and noise. However, prior channel state estimation and noise occur during the ZF process. The ZFE is advantageous for its simplicity and effectiveness in combating inter-symbol interference (ISI) in communication systems. By nullifying interference, it simplifies decoding at the receiver, enhancing signal quality. However, ZFE suffers from noise enhancement, making it susceptible to noise amplification and reducing its performance in noisy channels. In 6G, ZFE proves beneficial due to its low computational complexity, making it suitable for high-throughput and low-latency communications. With 6G’s emphasis on ultra-reliable and low-latency communication (URLLC) and massive connectivity, ZFE can provide efficient equalization, aiding in mitigating interference and improving spectral efficiency. Its simplicity aligns well with 6G’s goal of supporting diverse applications ranging from augmented reality to autonomous vehicles. The ZFE is subject to a few constraints51.
We consider an M-MIMO system with antennas at the transmitter and receiver. The M-MIMO system can be represented by Eq. (1):
$$Z=Hy+{\omega }_{n}.$$
(11)
The ZFE is applied to eliminate the interference between users by designing a linear transformation matrix (M). The matrix neutralizes the interference that occurs from the other user and enhances signal detection. The Rx signal after applying the ZFE can be expressed as follows52:
$${Z}_{ZFE}=H{y}^{M}+M{\omega }_{n}.$$
(12)
The ZFE should be designated such that matrix M satisfies the following condition:
where I denotes the identity matrix. The Eq. (13) ensures that the interference between users is completely eliminated.
MMSE
The MMSE is considered one of the most popular techniques for efficiently detecting signals in the presence of noise and interference. The MMMSE estimation offers several advantages in signal processing. It provides optimal estimates under Gaussian noise assumptions, effectively minimizing mean square error. MMSE estimation is computationally efficient and simpler to implement compared to other sophisticated techniques. It offers robustness against noise and can handle non-linear systems through iterative algorithms like the Expectation–Maximization (EM) algorithm. However, MMSE estimation relies heavily on accurate knowledge of statistical parameters and assumes linearity in the underlying system, limiting its applicability in highly non-linear scenarios. In the context of 6G, MMSE estimation holds promise due to its ability to effectively mitigate interference and noise, critical in high-density networks. Its computational efficiency makes it suitable for resource-constrained devices expected in 6G networks. Moreover, as 6G aims for ultra-reliable and low-latency communication, MMSE estimation’s ability to provide accurate estimates with minimal computational overhead aligns well with these requirements, facilitating efficient spectrum utilization and enhancing overall network performance53. Let us consider the mathematical model of M-MIMO represented by Eq. (1).
$$Z=Hy+{\omega }_{n}.$$
(14)
The goal of MMSE detection is to estimate the transmitted signal y given the received signal with all knowledge of the channel matrix H and noise statistics. The estimation of y, denoted as ŷ is given by44:
$$\widehat{y}=arg{\text{min}}yE\sum {\left|z-\widehat{z}\right|}^{2},$$
(15)
where E denotes the expectation operator. High complexity and prior knowledge of the channel are the few constraints of the MMSE.
Channel estimation proposed algorithms
Channel estimation is crucial for accurate signal detection in MIMO systems. This enables the receiver to estimate the characteristics of the wireless channel, including fading, interference, and spatial correlations. This information is essential for mitigating the effects of channel impairments, optimizing signal-detection algorithms, and achieving reliable communication performance under diverse environmental conditions. Accurate channel estimation enhances the system’s ability to separate the transmitted signals from noise and interference, leading to improved spectral efficiency, higher data rates, and enhanced overall system reliability in MIMO systems54.
Channel estimation QRM-MLD-ZF
The received signal at the receiver is represented as:
The QR decomposition of channel matrix is performed as:
MLD-ZF precoding aims to mitigate the interference by projecting the received signal onto the null space of the interference channels. The ZF precoding matrix F was computed as follows:
$$F={{(H}^{H}H)}^{-1}{ H}^{H},$$
(18)
where \({H}^{H}\) is the conjugate transpose of H. Channel matrix H can be estimated using a pilot symbol known at the receiver. Let \({Y}_{p}\) be the transmitted pilot symbols, and \({Z}_{p}\) be the received pilot symbols. Then, the estimated channel matrix \(\widetilde{H}\) can be obtained as
$$\widetilde{H}={Z}_{p}{Y}_{p}^{H}{\left({Y}_{p}^{H}{Y}_{p}\right)}^{-1}.$$
(19)
After estimating channel matrix \(\widetilde{H}\), it can be used for symbol detection. The received signal Z can be processed by MLD-ZF precoding as follows:
Then, MLD can be applied to detect the transmitted symbols Y based on the pre-processed received signal \({Z}^{ZF}\). Channel estimation is crucial for accurately estimating channel matrix H, which is essential for performing ZF precoding and subsequent symbol detection in the QRM-MLD-ZF algorithm55.
Channel estimation QRM-MLD-MMSE
Let us consider a MIMO system with \({N}_{t}\) and \({N}_{r}\) transmitting and receiving antennas, respectively. The received signal is given as
The QR decomposition is performed on the received signal matrix \(Z\) to obtain:
where Q is the orthogonal matrix and R is the upper triangular matrix. Substituting Q and R into the channel model, we obtain:
Pre-multiplying both side by \({Q}^{H}\), we have:
$${Q}^{H}QR={Q}^{H}HY+{Q}^{H}N.$$
(24)
Let us substitute \(I={Q}^{H}Q\), where \(I\) is the identity matrix and simplifies to
$$R={Q}^{H}HY+{Q}^{H}N.$$
(25)
The pilot symbols are typically transmitted to estimate the channel matrix H. Let \({Y}_{p}\) be the transmitted pilot symbols, and \({Z}_{p}\) be the received pilot symbols. Then, the estimated channel matrix \(\widetilde{H}\) can be obtained as
$${\widetilde{H}=(Q}^{H}{Y}_{p}){{(R}_{P})}^{-1},$$
(26)
where \({R}_{P}\) covariance matrix of the received pilot symbol \({Z}_{p}\). After estimating channel matrix \(\widetilde{H}\) it can be used for symbol detection. The MMSE detection method uses the estimated channel matrix to minimize the mean square error between the transmitted symbol \(Y\) and the detected symbol \(\widetilde{Y}\), given by
$$\widetilde{Y}={\widetilde{H}}^{H}{\left(\widetilde{H}{\widetilde{H}}^{H}+{\sigma }^{2}I\right)}^{-1}Z,$$
(27)
where \({\sigma }^{2}\) denotes the noise variance. Channel estimation in QRM-MLD-MMSE involves using QR decomposition to decompose the received signal matrix, estimating the channel matrix using pilot symbols, and then applying MMSE detection for symbol estimation based on the estimated channel matrix. This approach helps improve channel accuracy and symbol detection in the MIMO framework.


